Akustiske beregninger et eksempel

BILAG til BYG-ERFA bladet "Lyd- og støjforhold i skoler – efterklangstid og akustisk regulering" (99) 01 03 02

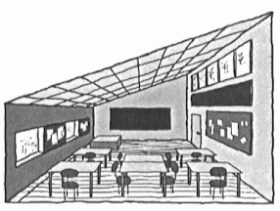
Grundplan 7 x 8 meter.

Lofthøjden varierer fra 2,7 m til 5,5 m.

Rumvolumenet er 258 m3.

Overflader:

22 mm trægulv på strøer

Vinduer med termoruder i den lave facade, samt vinduesbånd øverst i den høje væg ved samlingen med loftet

Vægge og brystning er lette pladevægge (2 lag 13 m gipsplade)

Lydabsorberende loft (20 mm porøs absorbent, nedhængt 200 mm)

Lydabsorbenter opsat øverst på den høje væg (40 mm porøs lavfrekvent absorbent, monteret direkte)

Lydabsorbenter udformet som opslagstavler (40 mm porøs absorbent, monteret direkte).

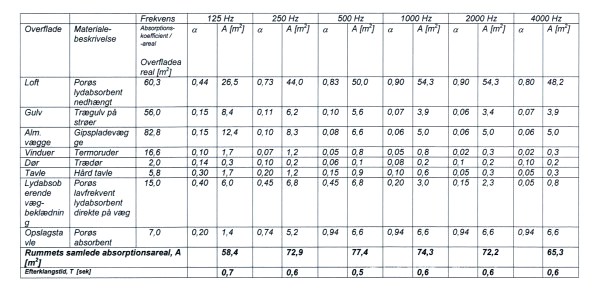
Absorptionskoefficient

Hver overflade i rummet bidrager til reguleringen af rummets efterklangstid. Hvor meget den enkelte overflade dæmper bestemmes af overfladematerialets absorptionskoefficient og areal.

Absorptionskoefficienten, a , er en talstørrelse mellem 0 og 1.

a = 0 betyder at materialet reflekterer al lyd, som rammer det - dvs. materialet har ingen lydabsorberende virkning.

a = 1 betyder at materialet absorberer al lyd, som rammer det.

Absorptionskoefficienten er afhængig af frekvensen.

Normalt vil en tynd lydabsorberende beklædning opsat direkte på et hårdt underlag give ringe lydabsorption (små a -værdier) ved lave frekvenser (basområdet), og relativt god lydabsorption (store a -værdier) ved høje frekvenser (diskantområdet).

Hvis man øger tykkelsen af materialet eller monterer den lydabsorberende beklædning foran et hulrum, vil lydabsorptionen ved lave frekvenser også øges.

Det er derfor nødvendigt at gennemføre efterklangsberegningerne i de 6 frekvensbånd fra 125 Hz til 4000 Hz.

Absorptionsarealet, A af en overflade findes ved at gange absorptionskoefficienten med fladens areal, S, dvs.

A = a x S. Man kan finde absorptionskoefficienter i byggevareleverandørernes informationsmaterialer, samt i faglitteraturreferencerne.

Nedenstående kolonner skal læses således:

Den førstnævnte flade "Trægulv" udgør et areal på 56 m2. Denne flade skal multipliceres med en række absorptionskoefficienter i de nævnte 6 frekvensbånd.

Ved 125 Hz er absorptionskoefficienten 0,15 og resultatet 56 x 0,15 = 8,4 m2 absorptionsareal.

Dernæst udføres tilsvarende beregninger for de øvrige frekvenser (vandret i skemaet) og for alle overfladerne i lokalet (lodret nedad i skemaet).

Til sidst summeres alle kolonnerne med absorptionsarealerne.

Efterklangstiden fremkommer så ved Sabines formel:

0,16 x Rumvolumen / Samlet absorptionsareal.

Rumvolumen, V = 258 m3.

Heraf fremgår, at såvel BR-95 kravene (gennemsnitsværdi af T i frekvensområdet 125 – 2000 Hz mindre end eller lig 0,9 sek.) som de anbefalede projekteringsværdier (T svarer til 0,6 sek. i hele frekvensområdet 125 – 4000 Hz) overholdes – bortset fra at efterklangstiden ved 125 Hz er længere end anbefalet.

I praksis vil efterklangstider med en enkelt afvigelse i denne størrelse ikke give anledning til brugsmæssige gener.

Bemærk:

Den anviste fremgangsmåde kan alene anvendes til overslagsberegninger i lokaler af almindelig størrelse.

Luftens lydabsorberende egenskaber er ikke indregnet i eksemplet – og specielt i store lokaler vil denne forenkling kunne føre til fejlagtige resultater.

Anvisning til "Gør-det-selv" beregning:

1. Lav et regneark som ovenstående skema.

2. Indsæt lokalets overflader og deres arealer.

3. Beskriv materialerne og indtast deres absorptionskoefficienter.

4. Beregn A = a x S

5. Summér A - søjle for søjle

6. Beregn efterklangstiden pr. 1/1-oktav (T = 0,16 x V / A)

7. Herefter har man lokalets efterklangstid pr. 1/1-oktav (i de 6 frekvensbånd)